久しぶりに数学の小ネタを。
よくあるやつですが・・・
13 - 12 = 1
⇔ 13 - 12 = 1 - 4 + 4
⇔ 9 + 4 - 12 = 1 - 4 + 4
⇔ 9 - 12 + 4 = 1 - 4 + 4
⇔ 9 - 2×3×2 + 4 = 1 - 2×2 + 4
⇔ (3 - 2)^2 = (1 - 2)^2
⇔ 3 - 2 = 1 - 2
⇔ 1 = -1
・・・!?
言うまでもないかもしれませんが、正しくは下の通り。
13 - 12 = 1
⇔ 13 - 12 = 1 - 4 + 4
⇔ 9 + 4 - 12 = 1 - 4 + 4
⇔ 9 - 12 + 4 = 1 - 4 + 4
⇔ 9 - 2×3×2 + 4 = 1 - 2×2 + 4
⇔ (3 - 2)^2 = (1 - 2)^2
⇔ |3 - 2| = |1 - 2| ←この絶対値(|で挟んでいる記号)がポイント。
⇔ 1 = |-1|
⇔ 1 = 1
両辺の平方根をとるときは符号に注意が必要です。
√(a - b)^2 = |a - b|
√(a + b)^2 = |a + b|
今日はこんなところです。Posted by hnfs.
よくあるやつですが・・・
13 - 12 = 1
⇔ 13 - 12 = 1 - 4 + 4
⇔ 9 + 4 - 12 = 1 - 4 + 4
⇔ 9 - 12 + 4 = 1 - 4 + 4
⇔ 9 - 2×3×2 + 4 = 1 - 2×2 + 4
⇔ (3 - 2)^2 = (1 - 2)^2
⇔ 3 - 2 = 1 - 2
⇔ 1 = -1
・・・!?
言うまでもないかもしれませんが、正しくは下の通り。
13 - 12 = 1
⇔ 13 - 12 = 1 - 4 + 4
⇔ 9 + 4 - 12 = 1 - 4 + 4
⇔ 9 - 12 + 4 = 1 - 4 + 4
⇔ 9 - 2×3×2 + 4 = 1 - 2×2 + 4
⇔ (3 - 2)^2 = (1 - 2)^2
⇔ |3 - 2| = |1 - 2| ←この絶対値(|で挟んでいる記号)がポイント。
⇔ 1 = |-1|
⇔ 1 = 1
両辺の平方根をとるときは符号に注意が必要です。
√(a - b)^2 = |a - b|
√(a + b)^2 = |a + b|
今日はこんなところです。Posted by hnfs.
-1^2 = ?
ここで、a^2は“aの2乗”を表すものとします。この日記の文法では指数がうまく書けないんですよね・・・
もちろん、答えは-1です。
なぜなら、-1^2は1^2に-1が掛けられている値、すなわち
-1^2 = -1×1^2
であるからです。
-1^2は-1を2回掛けるわけではありません。-1を2回掛けるときはカッコを用いて
(-1)^2
と表されます(このときはもちろん (-1)^2 = 1)。
これはルールです。数学の文法のようなもの。
なぜこんなことを書いたのかというと、中学1年生だった頃の1学期の中間テストで
-1^2 = 1
と解答してペケを喰らったことを急に思い出したからです。
当時は悔しかったです。
失点した原因が理解の不足よりもルールの覚え違いによる面が大きかったからです。
数学のテストでこんな減点をされるのが非常に理不尽に感じたあの頃のお話。
今日はこんなところです。Posted by hnfs.
ここで、a^2は“aの2乗”を表すものとします。この日記の文法では指数がうまく書けないんですよね・・・
もちろん、答えは-1です。
なぜなら、-1^2は1^2に-1が掛けられている値、すなわち
-1^2 = -1×1^2
であるからです。
-1^2は-1を2回掛けるわけではありません。-1を2回掛けるときはカッコを用いて
(-1)^2
と表されます(このときはもちろん (-1)^2 = 1)。
これはルールです。数学の文法のようなもの。
なぜこんなことを書いたのかというと、中学1年生だった頃の1学期の中間テストで
-1^2 = 1
と解答してペケを喰らったことを急に思い出したからです。
当時は悔しかったです。
失点した原因が理解の不足よりもルールの覚え違いによる面が大きかったからです。
数学のテストでこんな減点をされるのが非常に理不尽に感じたあの頃のお話。
今日はこんなところです。Posted by hnfs.
前提として。
a > 0 の場合、a の 0 乗(ここではa^0と書く)は 1 になります。
例えば、
3^0 = 1、11^0 = 1
となります。
この定義は、
2^4 = 2×2×2×2 = 16、
2^3 = 2×2×2 = 8、
2^2 = 2×2 = 4、
2^1 = 2
となることを考えれば妥当です。なぜなら、
2^3 = 2^4÷ 2、
2^2 = 2^3÷ 2、
2^1 = 2^2÷ 2
となっているので、
2^0 = 2^1÷ 2 = 1
となって整合性を保てるからです。
このように累乗を拡張していくと、マイナス乗に関しても、例えば
2^-1 = 1/2
のように定めることができます。
同様に、指数法則を用いても導けます。
指数法則とは
a^m + n = a^m×a^n
が成り立つ法則です。例えば、
2^4 = 2^1 + 3 = 2^1×2^3 = 2×8 = 16
となります。この法則で m = 0、n = 2、とすれば、
2^2 = 2^0 + 2 = 2^0×2^2
= 2^0×4
となるので、
2^0 = 2^2÷4 = 4 ÷4 = 1
となります。
ここで本題。タイトルにある「-1の-1乗」についてです。
最初のような定義で議論を進めていけば、
(-1)^2 = (-1)×(-1) = 1、
(-1)^1 = (-1)^2÷(-1) = 1÷(-1) = -1、
(-1)^0 = (-1)^1÷(-1) = -1÷(-1) = 1
となり、
(-1)^0 = 1
となることがわかります。指数法則を用いても、
(-1)^2 = (-1)0 + 2 = (-1)^0×(-1)2 = (-1)^0×1 = (-1)^0
より、
(-1)^0 = (-1)^2 = 1
を得ます。そうすると、
(-1)^1 = -1、(-1)^0 = 1
となっているのですから、
(-1)^-1 = (-1)^0÷(-1) = 1÷(-1) = -1 ・・・①
となるはず。ところで、指数法則で考えてみると、
(-1)^0 = (-1)^-1 + 1 = (-1)^1×(-1)^-1 = -1×(-1)^-1
となることから、
(-1)^-1 = (-1)^0÷(-1) = 1÷(-1) = -1
となってしまいます。これは、①と同じ結果ですね。
このように累乗は展開することができます。
今回は2通りの展開ができましたが、方に乗っている指数(^の右の小さい文字のこと)が分数や無理数(√2など)になると1番目のやり方では応用が利きません。それ以降は指数法則が成り立つことを前提にして、数列の収束などを使って一気に難しくなります。
ということで、今回はこの辺で。
ちなみに、マイナスの指数関数はとても複雑になっています。高校で習った y = a^x で a がマイナスになるとごちゃごちゃしたグラフになるのですが・・・
今日はこんなところです。Posted by hnfs.
この話の続きを書くことはないでしょうけどね。
a > 0 の場合、a の 0 乗(ここではa^0と書く)は 1 になります。
例えば、
3^0 = 1、11^0 = 1
となります。
この定義は、
2^4 = 2×2×2×2 = 16、
2^3 = 2×2×2 = 8、
2^2 = 2×2 = 4、
2^1 = 2
となることを考えれば妥当です。なぜなら、
2^3 = 2^4÷ 2、
2^2 = 2^3÷ 2、
2^1 = 2^2÷ 2
となっているので、
2^0 = 2^1÷ 2 = 1
となって整合性を保てるからです。
このように累乗を拡張していくと、マイナス乗に関しても、例えば
2^-1 = 1/2
のように定めることができます。
同様に、指数法則を用いても導けます。
指数法則とは
a^m + n = a^m×a^n
が成り立つ法則です。例えば、
2^4 = 2^1 + 3 = 2^1×2^3 = 2×8 = 16
となります。この法則で m = 0、n = 2、とすれば、
2^2 = 2^0 + 2 = 2^0×2^2
= 2^0×4
となるので、
2^0 = 2^2÷4 = 4 ÷4 = 1
となります。
ここで本題。タイトルにある「-1の-1乗」についてです。
最初のような定義で議論を進めていけば、
(-1)^2 = (-1)×(-1) = 1、
(-1)^1 = (-1)^2÷(-1) = 1÷(-1) = -1、
(-1)^0 = (-1)^1÷(-1) = -1÷(-1) = 1
となり、
(-1)^0 = 1
となることがわかります。指数法則を用いても、
(-1)^2 = (-1)0 + 2 = (-1)^0×(-1)2 = (-1)^0×1 = (-1)^0
より、
(-1)^0 = (-1)^2 = 1
を得ます。そうすると、
(-1)^1 = -1、(-1)^0 = 1
となっているのですから、
(-1)^-1 = (-1)^0÷(-1) = 1÷(-1) = -1 ・・・①
となるはず。ところで、指数法則で考えてみると、
(-1)^0 = (-1)^-1 + 1 = (-1)^1×(-1)^-1 = -1×(-1)^-1
となることから、
(-1)^-1 = (-1)^0÷(-1) = 1÷(-1) = -1
となってしまいます。これは、①と同じ結果ですね。
このように累乗は展開することができます。
今回は2通りの展開ができましたが、方に乗っている指数(^の右の小さい文字のこと)が分数や無理数(√2など)になると1番目のやり方では応用が利きません。それ以降は指数法則が成り立つことを前提にして、数列の収束などを使って一気に難しくなります。
ということで、今回はこの辺で。
ちなみに、マイナスの指数関数はとても複雑になっています。高校で習った y = a^x で a がマイナスになるとごちゃごちゃしたグラフになるのですが・・・
今日はこんなところです。Posted by hnfs.
この話の続きを書くことはないでしょうけどね。
今日は2011年5月24日。
20110524を素因数分解してみると、
20110524 = 2 × 2 × 3 × 13 × 83 × 163
となります。この桁数でこれだけの種類の素因数が出てくるのは大変珍しいことです。
素因数分解を手計算で行うとき、どの数で割り切れるかを簡単に知ることができると便利です。
というわけで、3の倍数の判定法を紹介しておきます。あまりにも有名なので知っている方も多いかもしれませんけどね。
さて。
ある数が3の倍数であるかどうかは、すべての桁を足し合わせた数が3の倍数であるかどうかで判定できます。
例えば、20110524。
2 + 0 + 1 + 1+ 0 + 5 + 2 + 4 = 15
であり、15は3の倍数なので、20110524は3の倍数となります。
また、2350は
2 + 3 + 5 + 0 = 10
であり、10は3の倍数ではないので、2350は3の倍数ではありません。
とまあこんな感じ。でもこれだけでは面白くないので、なぜそうなるのかを以下で簡単に証明してみます。
上の証明は4桁の数を扱いましたが、何桁の数でも同様にして証明できます。
ここで注意しておきたいことは、上はあくまでも
「各桁の和が3の倍数」⇒「その数は3の倍数」
であることを証明したに過ぎず、決して
「各桁の和が3の倍数ではない」⇒「その数は3の倍数ではない」
ということが証明されたわけではありません。また、この反対(逆)である
「3の倍数である」⇒「その数の各桁の和は3の倍数」
であることも証明されたわけではありません。
一応、上と似たような方法でこれらのことも証明できます。
長くなってしまいました。
今日はこんなところです。Posted by hnfs.
20110524を素因数分解してみると、
20110524 = 2 × 2 × 3 × 13 × 83 × 163
となります。この桁数でこれだけの種類の素因数が出てくるのは大変珍しいことです。
素因数分解を手計算で行うとき、どの数で割り切れるかを簡単に知ることができると便利です。
というわけで、3の倍数の判定法を紹介しておきます。あまりにも有名なので知っている方も多いかもしれませんけどね。
さて。
ある数が3の倍数であるかどうかは、すべての桁を足し合わせた数が3の倍数であるかどうかで判定できます。
例えば、20110524。
2 + 0 + 1 + 1+ 0 + 5 + 2 + 4 = 15
であり、15は3の倍数なので、20110524は3の倍数となります。
また、2350は
2 + 3 + 5 + 0 = 10
であり、10は3の倍数ではないので、2350は3の倍数ではありません。
とまあこんな感じ。でもこれだけでは面白くないので、なぜそうなるのかを以下で簡単に証明してみます。
上に挙げた2350は、
2 × 1000 + 3 × 100 + 5 × 10
と分解することができます。同様に、2011は
2 × 1000 + 1 × 10 + 1
と分解できます。このようにして、すべての4桁の数(整数)は一般に
a × 1000 + b × 100 + c × 10 + d
の形に分解できます。この表示方法を使います。
今、各桁の数の和は3の倍数であるとします。すると、上の表示でいえば a + b + c + d が3の倍数であると言えます。よって、n (整数)を使って
a + b + c + d = 3 × n ・・・①
と表すことができます。すると、
a × 1000 + b × 100 + c × 10 + d
= (a × 999 + a) + (b × 99 + b) + (c × 9 + c) + d
= (a × 999 + b × 99 + c × 9) + a + b + c + d
= 3(a × 333 + b × 33 + c × 3) + 3 × n
= 3 (a × 333 + b × 33 + c × 3 + n)
と書き直すことができます。青部分は式①を使って赤部分の式に書き直せるからです。
一番下の式を見てみると、これは 「3 × * 」の形をしているので3の倍数、すなわち、a × 1000 + b × 100 + c × 10 + d が3の倍数であることが分かったわけです。
上の証明は4桁の数を扱いましたが、何桁の数でも同様にして証明できます。
ここで注意しておきたいことは、上はあくまでも
「各桁の和が3の倍数」⇒「その数は3の倍数」
であることを証明したに過ぎず、決して
「各桁の和が3の倍数ではない」⇒「その数は3の倍数ではない」
ということが証明されたわけではありません。また、この反対(逆)である
「3の倍数である」⇒「その数の各桁の和は3の倍数」
であることも証明されたわけではありません。
一応、上と似たような方法でこれらのことも証明できます。
長くなってしまいました。
今日はこんなところです。Posted by hnfs.
2011年。
2011の2、0、1、1を並べ替えると、最大で2110、最小で0112(= 112)となります。
最大から最小を引いてみると・・・
2110 - 0112 = 1998。
1988の1、9、8、8を並べ替えると、最大で9811、最小で1189。
引くと、
9811 - 1189 = 8082。
同様に、
8820 - 0288 = 8532、
8532 - 2358 = 6174。
この操作をカプレカ操作というようです。では、6174についても続けてカプレカしてみましょう。でも・・・
7641 - 1467 = 6174。
また6174になります。ということは、これ以上カプレカ操作を続けても永遠に6174が出続けることになります。
6174のように、桁を並び替えて最大数から最小数を引いたとき、元の数に戻る数はカプレカ数と呼ばれています。カプレカ数は他にもまったく異なる定義があるそうですが、ここではそんなこと気にしません。
カプレカ数は他に、
0、495、(6174)、549945631764、・・・などがあります。
4桁から一気に12桁に飛ぶんですねぇ
カプレカ数でない他の数について、たとえば12345については
54321 - 12345 = 41976
97641 - 14679 = 82962
98622 - 22689 = 75933
97533 - 33579 = 63954
96543 - 34569 = 61974
97641 - 14679 = 82962
となり、「82962→75933→63954→61974→82962→・・・」というサイクルが出てくることがわかります。
よくよく考えてみれば当たり前なことです。
どんな数(たとえば 11 桁の数)にカプレカ操作を施しても、高々10 の 11 乗通りの数(00000000000 ~ 99999999999)しか現れません。
よって、少なくとも「10 の 11 乗」+ 1 = 100000000001回カプレカ数を繰り返せば(相当膨大な回数ですが・・・)、最低でも1つの数については重複することとなってしまいます(上の例の82962のように)。
そこからサイクルを作ることができますね。
一つの数でサイクルが閉じているパターンが 6174 のようなカプレカ数となっています。
さて。
6174は4桁のカプレカ数ですが、実はどの4桁の数もカプレカ操作を繰り返せば 0 か 6174 に戻るらしいです。
さらに、495は3桁のカプレカ数ですが、いくつかの数字で確認したところ、どれもカプレカ操作を繰り返せば 0 または 495 にたどり着いてしまいました。
3桁の数はすべてがカプレカ操作により 0 または 495 にたどり着くのでしょうか?
(→追記:確認してみたところ、そのとおりでした。0 または 495 になります。)
カプレカ数が存在する桁の数はどんな数でもカプレカ操作により 0 またはそのカプレカ数にたどり着くことができるのでしょうか?
調べもせず証明もせず申し訳ありませんが、知っている方がいたら教えてください。
今日はこんなところです。Posted by hnfs.
2011の2、0、1、1を並べ替えると、最大で2110、最小で0112(= 112)となります。
最大から最小を引いてみると・・・
2110 - 0112 = 1998。
1988の1、9、8、8を並べ替えると、最大で9811、最小で1189。
引くと、
9811 - 1189 = 8082。
同様に、
8820 - 0288 = 8532、
8532 - 2358 = 6174。
この操作をカプレカ操作というようです。では、6174についても続けてカプレカしてみましょう。でも・・・
7641 - 1467 = 6174。
また6174になります。ということは、これ以上カプレカ操作を続けても永遠に6174が出続けることになります。
6174のように、桁を並び替えて最大数から最小数を引いたとき、元の数に戻る数はカプレカ数と呼ばれています。カプレカ数は他にもまったく異なる定義があるそうですが、ここではそんなこと気にしません。
カプレカ数は他に、
0、495、(6174)、549945631764、・・・などがあります。
4桁から一気に12桁に飛ぶんですねぇ
カプレカ数でない他の数について、たとえば12345については
54321 - 12345 = 41976
97641 - 14679 = 82962
98622 - 22689 = 75933
97533 - 33579 = 63954
96543 - 34569 = 61974
97641 - 14679 = 82962
となり、「82962→75933→63954→61974→82962→・・・」というサイクルが出てくることがわかります。
よくよく考えてみれば当たり前なことです。
どんな数(たとえば 11 桁の数)にカプレカ操作を施しても、高々10 の 11 乗通りの数(00000000000 ~ 99999999999)しか現れません。
よって、少なくとも「10 の 11 乗」+ 1 = 100000000001回カプレカ数を繰り返せば(相当膨大な回数ですが・・・)、最低でも1つの数については重複することとなってしまいます(上の例の82962のように)。
そこからサイクルを作ることができますね。
一つの数でサイクルが閉じているパターンが 6174 のようなカプレカ数となっています。
さて。
6174は4桁のカプレカ数ですが、実はどの4桁の数もカプレカ操作を繰り返せば 0 か 6174 に戻るらしいです。
さらに、495は3桁のカプレカ数ですが、いくつかの数字で確認したところ、どれもカプレカ操作を繰り返せば 0 または 495 にたどり着いてしまいました。
3桁の数はすべてがカプレカ操作により 0 または 495 にたどり着くのでしょうか?
(→追記:確認してみたところ、そのとおりでした。0 または 495 になります。)
カプレカ数が存在する桁の数はどんな数でもカプレカ操作により 0 またはそのカプレカ数にたどり着くことができるのでしょうか?
調べもせず証明もせず申し訳ありませんが、知っている方がいたら教えてください。
今日はこんなところです。Posted by hnfs.
1/7 = 0.142857142857142857142857………
2/7 = 0.285714285714285714285714………
3/7 = 0.428571428571428571428571………
4/7 = 0.571428571428571428571428………
5/7 = 0.714285714285714285714285………
6/7 = 0.857142857142857142857142………
お久しぶりです。hnfsです。
いつの間にか年が明けたようで、2011年です。
今年も温かい目で見守ってください。よろしくお願いします。
上の式について。
1/7 ~ 6/7 は有限小数では表しきれません。循環小数になります。
しかし、この6つの循環小数を見比べてみると、どれも「…142857…」の並びで循環していることが分かります。
ざっと 50 ぐらいまで確認しましたけど、1/7 ほど面白いのは見つかりませんでした。
それで。
1/7 の循環小数表示には、3、6、9が出てきません。これはなぜなのでしょうか? 3 つとも 3 の倍数なのが意味ありげですね。
ちょっと考えてみました。
1/7 を筆算してみると気づきますが、どの段階においても 10 の倍数を 7 で割る必要が出てきます。
そのときの商は、3、6、9 にはなりえません。なぜならば、
7×3 = 21、7×4 = 28
7×6 = 42、7×7 = 49
より、30 や 50 を 7 で割るときは 3 や 6 でなく、4 や 7 の方が採用されるからです。また、7 で割るときの余りは 1 ~ 6 のいずれかになるので、この筆算で 60 より大きい数を割ることは起こりえません。7×9 = 63 なので、9 は出てこないことが分かります。
・・・
あまりエレガントではありませんね。
もしかしたら、3の倍数と7とにもっと密接な関係があって、そこから導き出せるかもしれません。
まぁでも、7で割った余りは 1 ~ 6 のいづれかなのですから、循環のサイクルの長さも高々6 なわけで、現れない数字が3つあっても不思議ではないのですけどね。
142 + 857 = 999、142857×7 = 999999、・・・etc.
この辺で止めておきましょう。
この数字にはもっといろいろあるようです。興味があれば「1/7 循環小数」で検索。カチッ
今日はこんなところです。Posted by hnfs.
2/7 = 0.285714285714285714285714………
3/7 = 0.428571428571428571428571………
4/7 = 0.571428571428571428571428………
5/7 = 0.714285714285714285714285………
6/7 = 0.857142857142857142857142………
お久しぶりです。hnfsです。
いつの間にか年が明けたようで、2011年です。
今年も温かい目で見守ってください。よろしくお願いします。
上の式について。
1/7 ~ 6/7 は有限小数では表しきれません。循環小数になります。
しかし、この6つの循環小数を見比べてみると、どれも「…142857…」の並びで循環していることが分かります。
ざっと 50 ぐらいまで確認しましたけど、1/7 ほど面白いのは見つかりませんでした。
それで。
1/7 の循環小数表示には、3、6、9が出てきません。これはなぜなのでしょうか? 3 つとも 3 の倍数なのが意味ありげですね。
ちょっと考えてみました。
1/7 を筆算してみると気づきますが、どの段階においても 10 の倍数を 7 で割る必要が出てきます。
そのときの商は、3、6、9 にはなりえません。なぜならば、
7×3 = 21、7×4 = 28
7×6 = 42、7×7 = 49
より、30 や 50 を 7 で割るときは 3 や 6 でなく、4 や 7 の方が採用されるからです。また、7 で割るときの余りは 1 ~ 6 のいずれかになるので、この筆算で 60 より大きい数を割ることは起こりえません。7×9 = 63 なので、9 は出てこないことが分かります。
・・・
あまりエレガントではありませんね。
もしかしたら、3の倍数と7とにもっと密接な関係があって、そこから導き出せるかもしれません。
まぁでも、7で割った余りは 1 ~ 6 のいづれかなのですから、循環のサイクルの長さも高々6 なわけで、現れない数字が3つあっても不思議ではないのですけどね。
142 + 857 = 999、142857×7 = 999999、・・・etc.
この辺で止めておきましょう。
この数字にはもっといろいろあるようです。興味があれば「1/7 循環小数」で検索。カチッ
今日はこんなところです。Posted by hnfs.
記数法 :『零の発見 -数学の生い立ち-』
2010年8月22日 数学
数年前、人からもらった本。
前半だけしか読んでいないままほったらかしにしていたため、最初のほうから久しぶりに読み返してみました。
2部構成になっていて、前半は零の発見による記数法に関する内容が中心でした。
今使われている記数法は便利ですよね。0 ~ 9 の10 種類の数字だけで、どんなに大きな数も(そして小さな数も)表すことができます。
例えば、世界の人口を表す六十八億八千八百三十万五千八百五十二(推計)を
6888305852
と書くように。http://arkot.com/jinkou/
ちなみに、世界の人口は刻一刻と変化しているので現在の数字とは異なります。
紀元前5世紀ごろのギリシャの記数法なんて、今の記数法と比べればややこしいばかり。
http://www.infonet.co.jp/apt/march/syllabus/bookshelf/G/Greek.html
なるほど、こんな煩わしい記数法では代数学が発展しなかったのもうなずけます。
大きな数を表すにはより多くの種類のアルファベットを用意しなければなりませんからね。
この記数法は数字の記述以外にも、とくに筆算に強いということも大事なところです。
位取りがあるということは便利なんですね。これも 0 のおかげか。
記数法以外にも、2進法や無限級数、そして循環小数・無理数の話も出てきます。
他にもそろばんの話や歴史的な背景の話も出てきたのですが、そこには正直興味はなかったかな。
ちょっと古い言葉の使い方なども、本書の年季を表す材料になっていていいんじゃないでしょうか。
後半はまだ読んでいません。
興味のある方は以下を参考に。
http://www.amazon.co.jp/%E9%9B%B6%E3%81%AE%E7%99%BA%E8%A6%8B%E2%80%95%E6%95%B0%E5%AD%A6%E3%81%AE%E7%94%9F%E3%81%84%E7%AB%8B%E3%81%A1-%E5%B2%A9%E6%B3%A2%E6%96%B0%E6%9B%B8-%E5%90%89%E7%94%B0-%E6%B4%8B%E4%B8%80/dp/4004000130
今日はこんなところです。Posted by hnfs.
前半だけしか読んでいないままほったらかしにしていたため、最初のほうから久しぶりに読み返してみました。
2部構成になっていて、前半は零の発見による記数法に関する内容が中心でした。
今使われている記数法は便利ですよね。0 ~ 9 の10 種類の数字だけで、どんなに大きな数も(そして小さな数も)表すことができます。
例えば、世界の人口を表す六十八億八千八百三十万五千八百五十二(推計)を
6888305852
と書くように。http://arkot.com/jinkou/
ちなみに、世界の人口は刻一刻と変化しているので現在の数字とは異なります。
紀元前5世紀ごろのギリシャの記数法なんて、今の記数法と比べればややこしいばかり。
http://www.infonet.co.jp/apt/march/syllabus/bookshelf/G/Greek.html
なるほど、こんな煩わしい記数法では代数学が発展しなかったのもうなずけます。
大きな数を表すにはより多くの種類のアルファベットを用意しなければなりませんからね。
この記数法は数字の記述以外にも、とくに筆算に強いということも大事なところです。
位取りがあるということは便利なんですね。これも 0 のおかげか。
記数法以外にも、2進法や無限級数、そして循環小数・無理数の話も出てきます。
他にもそろばんの話や歴史的な背景の話も出てきたのですが、そこには正直興味はなかったかな。
ちょっと古い言葉の使い方なども、本書の年季を表す材料になっていていいんじゃないでしょうか。
後半はまだ読んでいません。
興味のある方は以下を参考に。
http://www.amazon.co.jp/%E9%9B%B6%E3%81%AE%E7%99%BA%E8%A6%8B%E2%80%95%E6%95%B0%E5%AD%A6%E3%81%AE%E7%94%9F%E3%81%84%E7%AB%8B%E3%81%A1-%E5%B2%A9%E6%B3%A2%E6%96%B0%E6%9B%B8-%E5%90%89%E7%94%B0-%E6%B4%8B%E4%B8%80/dp/4004000130
今日はこんなところです。Posted by hnfs.
ようやく「1章・体の理論」終了
2010年8月4日 数学
ガロア理論をやってみようと思い、右上の本「体とガロア理論 - 桂利行 著」を読んでいます。
ノートを見ていたら、始めたのは何と6月頭。
で、今は8月頭。
2ヵ月かかって1章を読み上げたことになりますね・・・。
まぁガロアばっかりに時間を取るわけにもいかなかったし、途中約1ヵ月ほどは完全にやらなかったからな~
焦って勉強しなければいけないもんでもないですし、ゆっくりやっていくことにします。
「そんなんじゃイカン!」なんてお咎めはご勘弁ください…
しかし、この本の補足・補完として右下の別の本「ガロア理論 その標準的な入門 - 中野伸 著」を使っていたのですが、実際には2冊の本を同時並行で読む形になってしまいました。
例えば、正規拡大。
正規拡大であることの必要十分条件に関する定理の証明で「体とガロア理論」では意味不明なところを中野さんの本で補足しようとしたのですが、なんと正規拡大の定義が両者で異なる!
そのため証明のアプローチが異なり、しかもその証明は他の定理や補題の引用が多いので、結局中野さんの本も始めのほうから(必要な部分だけ)読み返すことに。
ま、数学ではよくある話ですけどね!
あ、もちろん正規拡大の定義は「体とガロア理論」のそれと「ガロア理論」のそれとは同値、つまり一致することが証明できますよ!
ただ、文面が異なるんですね。
ガロア拡大を定義したあたりから、証明の補完が難しくなってきました。
超越拡大の項は目的から少し逸れるので、流し読みで済ませてしまいました。
次章からはガロア群の計算や方程式のベキ根の話がでてくるそうなので、楽しみである反面余計難しくなりそうだ・・・
今回は1章を終えた感想だけになりましたが、またその気になれば1章のまとめをサラッと書き記すかもしれません。
今日はこんなところです。Posted by hnfs.
ノートを見ていたら、始めたのは何と6月頭。
で、今は8月頭。
2ヵ月かかって1章を読み上げたことになりますね・・・。
まぁガロアばっかりに時間を取るわけにもいかなかったし、途中約1ヵ月ほどは完全にやらなかったからな~
焦って勉強しなければいけないもんでもないですし、ゆっくりやっていくことにします。
「そんなんじゃイカン!」なんてお咎めはご勘弁ください…
しかし、この本の補足・補完として右下の別の本「ガロア理論 その標準的な入門 - 中野伸 著」を使っていたのですが、実際には2冊の本を同時並行で読む形になってしまいました。
例えば、正規拡大。
正規拡大であることの必要十分条件に関する定理の証明で「体とガロア理論」では意味不明なところを中野さんの本で補足しようとしたのですが、なんと正規拡大の定義が両者で異なる!
そのため証明のアプローチが異なり、しかもその証明は他の定理や補題の引用が多いので、結局中野さんの本も始めのほうから(必要な部分だけ)読み返すことに。
ま、数学ではよくある話ですけどね!
あ、もちろん正規拡大の定義は「体とガロア理論」のそれと「ガロア理論」のそれとは同値、つまり一致することが証明できますよ!
ただ、文面が異なるんですね。
ガロア拡大を定義したあたりから、証明の補完が難しくなってきました。
超越拡大の項は目的から少し逸れるので、流し読みで済ませてしまいました。
次章からはガロア群の計算や方程式のベキ根の話がでてくるそうなので、楽しみである反面余計難しくなりそうだ・・・
今回は1章を終えた感想だけになりましたが、またその気になれば1章のまとめをサラッと書き記すかもしれません。
今日はこんなところです。Posted by hnfs.
周知のように、πとは円周率のことです。
ふと思い出したんですけど、
昔、私が高校生だった頃、とある大学の数学の受験問題にπの値を近似する問題が出題されていました。
その解答の半分はだいたいこんな感じ。
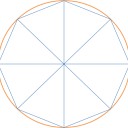
図のように、半径1の円を正多角形(図では正八角形)に外接させます。
このとき、もちろん円の面積は
半径 × 半径 × 円周率 = 1 × 1 × π = π。
一方、円の内部の正多角形(ここでは図の正八角形で計算)の面積は
小三角形の面積 × 8 = 1/2 × 1 × 1 × sin45°× 8
= 1/2 × 1/√2 × 8
= 2√2
≒ 2 × 1.41421356
= 2.82842712。
図が表すように、正多角形の面積は円の面積の大部分を覆っています。
(画像の左右の端が少し切れてしまっているのはご愛嬌です。)
よって、
(円の面積) ≒ (多角形の面積)
と考えると
π ≒ 2.82842712
となります。
しかし。
π = 3.
1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 ・・・
となります(どうやら無限に不規則に続いていくようです)。
ちなみに、これは小数点第 1000 位までの値です。
大雑把に
π = 3.14159265
とみなしても、
3.14159265 = π ≒ 2.82842712
となり、この近似ではまだまだ精度が低いということが分かります。
あの多角形と円の隙間の面積が 0.32 ぐらいなんですね。
今回はπの下からの評価でした。
つまり、 2.82842712 < π。
実はこの問題、円を多角形に内接させて上からのπの数値の評価もすればπの値の範囲が分かります。
以上、なかなかうまくいかない例を挙げてみました。
興味のある方は次のリンクをどうぞ。
http://hp.vector.co.jp/authors/VA014765/pi/howto.html
今回の方法はリンクの「再帰的に円周率を求める方法」にあたります。
今日はこんなところです。Posted by hnfs.
ふと思い出したんですけど、
昔、私が高校生だった頃、とある大学の数学の受験問題にπの値を近似する問題が出題されていました。
その解答の半分はだいたいこんな感じ。
図のように、半径1の円を正多角形(図では正八角形)に外接させます。
このとき、もちろん円の面積は
半径 × 半径 × 円周率 = 1 × 1 × π = π。
一方、円の内部の正多角形(ここでは図の正八角形で計算)の面積は
小三角形の面積 × 8 = 1/2 × 1 × 1 × sin45°× 8
= 1/2 × 1/√2 × 8
= 2√2
≒ 2 × 1.41421356
= 2.82842712。
図が表すように、正多角形の面積は円の面積の大部分を覆っています。
(画像の左右の端が少し切れてしまっているのはご愛嬌です。)
よって、
(円の面積) ≒ (多角形の面積)
と考えると
π ≒ 2.82842712
となります。
しかし。
π = 3.
1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 ・・・
となります(どうやら無限に不規則に続いていくようです)。
ちなみに、これは小数点第 1000 位までの値です。
大雑把に
π = 3.14159265
とみなしても、
3.14159265 = π ≒ 2.82842712
となり、この近似ではまだまだ精度が低いということが分かります。
あの多角形と円の隙間の面積が 0.32 ぐらいなんですね。
今回はπの下からの評価でした。
つまり、 2.82842712 < π。
実はこの問題、円を多角形に内接させて上からのπの数値の評価もすればπの値の範囲が分かります。
以上、なかなかうまくいかない例を挙げてみました。
興味のある方は次のリンクをどうぞ。
http://hp.vector.co.jp/authors/VA014765/pi/howto.html
今回の方法はリンクの「再帰的に円周率を求める方法」にあたります。
今日はこんなところです。Posted by hnfs.
グリゴリー・ペレルマン 賞金受け取りを断る
2010年7月5日 数学
数学の難問の1つである「ポアンカレ予想」を解決したロシア人数学者・グレゴリーペレルマン。
何年か前にNHKの番組でも取り上げられていたようで、ご存知の方も多いでしょう。
ちなみにその「ポアンカレ予想」とは
というものです。
単連結や多様体はざっくりとならばイメージできるものの、3次元球面などという4次元世界の創造力を要する高度な対象を良く取り扱えたものです。
ポアンカレ予想は3次元球面についての主張となっていますが、4次元以上の球面について成り立つことは早くから証明されていたようです。
この予想には3次元ならではの難しさがあったんでしょうね。
そしてこのこともご存知かもしれませんが、実はポアンカレ予想はミレニアム懸賞問題の1つであり、証明したものに100万ドルの賞金が与えられることになっていました。
そして今回のタイトル。
ペレルマンは賞金の受け取りを断ったそうです。携帯のニュースフラッシュに配信されるほどのニュースなのでご存知の方も多いかと。
理由はいろいろあるようですけど。
http://ja.wikipedia.org/wiki/%E3%83%9D%E3%82%A2%E3%83%B3%E3%82%AB%E3%83%AC%E4%BA%88%E6%83%B3#.E8.B3.9E.E9.87.91100.E4.B8.87.E3.83.89.E3.83.AB
数学界の決定の不公平さなどが理由であるらしい。これからいろいろ議論を呼びそうですね。
実はポアンカレ予想について書かれた単行本を持っているのですが、まだ読み切っていません・・・。
いずれ時間を見つけてまた最初から読んでみたいと思います。
右上の画像がその単行本です。
今日はこんなところです。Posted by hnfs.
何年か前にNHKの番組でも取り上げられていたようで、ご存知の方も多いでしょう。
ちなみにその「ポアンカレ予想」とは
単連結な3次元閉多様体は3次元球面に同相である
というものです。
単連結や多様体はざっくりとならばイメージできるものの、3次元球面などという4次元世界の創造力を要する高度な対象を良く取り扱えたものです。
ポアンカレ予想は3次元球面についての主張となっていますが、4次元以上の球面について成り立つことは早くから証明されていたようです。
この予想には3次元ならではの難しさがあったんでしょうね。
そしてこのこともご存知かもしれませんが、実はポアンカレ予想はミレニアム懸賞問題の1つであり、証明したものに100万ドルの賞金が与えられることになっていました。
そして今回のタイトル。
ペレルマンは賞金の受け取りを断ったそうです。携帯のニュースフラッシュに配信されるほどのニュースなのでご存知の方も多いかと。
理由はいろいろあるようですけど。
http://ja.wikipedia.org/wiki/%E3%83%9D%E3%82%A2%E3%83%B3%E3%82%AB%E3%83%AC%E4%BA%88%E6%83%B3#.E8.B3.9E.E9.87.91100.E4.B8.87.E3.83.89.E3.83.AB
数学界の決定の不公平さなどが理由であるらしい。これからいろいろ議論を呼びそうですね。
実はポアンカレ予想について書かれた単行本を持っているのですが、まだ読み切っていません・・・。
いずれ時間を見つけてまた最初から読んでみたいと思います。
右上の画像がその単行本です。
今日はこんなところです。Posted by hnfs.
最近、代数学の勉強を始めてみました。
代数学とは、数やモノの集まり(集合)の構造を調べる学問のことです。
目的は、大学での学部の講義で全く分からなかった Galois(「ガロア」、と読む) の制覇です。興味はあったのですが、当時はさっぱりわからなかった。
ちなみに、「Algebra」とは「代数(学)」の英訳です。
Galois 理論によって角度の三等分の作図は不可能であることが証明されたり、3次、4次方程式の“解”の公式が導けることもそうですが・・・
これ以上はあえて伏せておきましょう。
「解」に違和感を持ったそこのアナタ!通ですね。
片手間の勉強なので今後どれだけ力を入れていけるかわかりませんが、こうして日記に書くことによってモチベーションが高められそうなのでわざわざ記事にしてみました。
それだけです。
今日はただ日記を更新したかっただけなので、中身はこれだけです。
今日はこんなところです。Posted by hnfs.
代数学とは、数やモノの集まり(集合)の構造を調べる学問のことです。
目的は、大学での学部の講義で全く分からなかった Galois(「ガロア」、と読む) の制覇です。興味はあったのですが、当時はさっぱりわからなかった。
ちなみに、「Algebra」とは「代数(学)」の英訳です。
Galois 理論によって角度の三等分の作図は不可能であることが証明されたり、3次、4次方程式の“解”の公式が導けることもそうですが・・・
これ以上はあえて伏せておきましょう。
「解」に違和感を持ったそこのアナタ!通ですね。
片手間の勉強なので今後どれだけ力を入れていけるかわかりませんが、こうして日記に書くことによってモチベーションが高められそうなのでわざわざ記事にしてみました。
それだけです。
今日はただ日記を更新したかっただけなので、中身はこれだけです。
今日はこんなところです。Posted by hnfs.
数学が得意、または好き、という人は周りに結構いると思います。
しかし、その人は必ずしも数学のすべての分野に対して得意、または好き、という訳ではないと思うのです。
ただし、ごく一部の超人は除く。
例えば、多くの人が(もしかしたらいやいやながらも)勉強してきたであろう、センター試験の数学。
数学Ⅰ・Aとかだと、二次関数・三角比・確率が出題されたと思います。受験年度によっては数列もありますね。
私の身の回りには、
「三角比や二次関数はよくわからんけど、確率は数え上げればできるぜ!」って人や
「確率はゴチャゴチャして面倒だ。すっきりと解ける数列や二次関数が楽だよ!」って人など、
各人の思考回路というべきものが色濃くでていたように思います。
(ちなみに私は後者です)
数学Ⅱ・Bに関しても、出題範囲である対数関数・三角関数・微分積分・ベクトル、年度によっては複素数平面や数列があったり、選択によってはここでも確率の問題を解くことができます。ここでも、
「訳分からん難しいベクトルより、確率が解きやすいでしょ!」とか、
逆に確率なんて最初から眼中にない人までいます。(←多分このパターンが大多数)
(ご多分にもれず、ここでも私は後者でした)
更に例をあげるとすれば、大学の数学でも。
イメージしやすい微分幾何や位相幾何、結び目を得意とする人や、
抽象的理論でゴチャゴチャ式をこねくり回す代数屋さん、
実データを解析して、なんらかの傾向を見つける統計学の人、
代数・幾何・解析の知識を用いて関数空間をいじくる作用素環など、
いろいろな考え方があります。
(これら数学の諸分野の内容はあくまでも私の個人的な捉え方です。)
数学を専攻している人の中にも得意・不得意、好き・嫌いがあるのです。
何が言いたいかというと、
人にはそれぞれ向き不向きがあると思うので、今取り組んでいることがうまくいかなくても、それは「自分には向いていないんだ」という逃げ道が作れるんだということです。
でもだからこそ、自分に向いている、自分の思考回路にそっていることをしっかり見分けなければならないのですね。
そうでないと、つまり自分に不向きなことに取り組み続けていると、苦労が絶えないでしょうね。
なんだかまとまっていないけど、数学を糸口にこんなことを書いてしまいました。
何書いているんだろ・・・
別に病んでなんかいないですよ!
今日はこんなところです。Posted by hnfs.
しかし、その人は必ずしも数学のすべての分野に対して得意、または好き、という訳ではないと思うのです。
ただし、ごく一部の超人は除く。
例えば、多くの人が(もしかしたらいやいやながらも)勉強してきたであろう、センター試験の数学。
数学Ⅰ・Aとかだと、二次関数・三角比・確率が出題されたと思います。受験年度によっては数列もありますね。
私の身の回りには、
「三角比や二次関数はよくわからんけど、確率は数え上げればできるぜ!」って人や
「確率はゴチャゴチャして面倒だ。すっきりと解ける数列や二次関数が楽だよ!」って人など、
各人の思考回路というべきものが色濃くでていたように思います。
(ちなみに私は後者です)
数学Ⅱ・Bに関しても、出題範囲である対数関数・三角関数・微分積分・ベクトル、年度によっては複素数平面や数列があったり、選択によってはここでも確率の問題を解くことができます。ここでも、
「訳分からん難しいベクトルより、確率が解きやすいでしょ!」とか、
逆に確率なんて最初から眼中にない人までいます。(←多分このパターンが大多数)
(ご多分にもれず、ここでも私は後者でした)
更に例をあげるとすれば、大学の数学でも。
イメージしやすい微分幾何や位相幾何、結び目を得意とする人や、
抽象的理論でゴチャゴチャ式をこねくり回す代数屋さん、
実データを解析して、なんらかの傾向を見つける統計学の人、
代数・幾何・解析の知識を用いて関数空間をいじくる作用素環など、
いろいろな考え方があります。
(これら数学の諸分野の内容はあくまでも私の個人的な捉え方です。)
数学を専攻している人の中にも得意・不得意、好き・嫌いがあるのです。
何が言いたいかというと、
人にはそれぞれ向き不向きがあると思うので、今取り組んでいることがうまくいかなくても、それは「自分には向いていないんだ」という逃げ道が作れるんだということです。
でもだからこそ、自分に向いている、自分の思考回路にそっていることをしっかり見分けなければならないのですね。
そうでないと、つまり自分に不向きなことに取り組み続けていると、苦労が絶えないでしょうね。
なんだかまとまっていないけど、数学を糸口にこんなことを書いてしまいました。
何書いているんだろ・・・
別に病んでなんかいないですよ!
今日はこんなところです。Posted by hnfs.
素数のお話 ~平方数への分解~
2010年4月27日 数学 コメント (2)素数ってご存知ですよね?
整数 p が素数であるとは、
p が 1または p 自身以外に約数を持たないことを言います。
たとえば、2 の約数は 1 と 2 のみなので、2 は素数です。
そして、13 や 71 なども素数になります。
逆に、4 は 2 を約数に持つ(すなわち、1 と自分自身の 4 以外の約数を持つ)ので、素数ではありません。ちなみに、1 も素数ではないと約束します。
この素数とやらは数々の魅力的な性質を持っており、これまで多くの数学者を虜にしてきたようです。
そこで、今回はその不思議な性質の 1 つを紹介したいと思います。
素数をいくつか列挙してみます。
2、3、5、7、11、13、17、19、23、29、31…
これくらいにしておきましょう。
これらの素数のうち、
5、13、17、29
には、ある性質があります。
それは、
5 = 1^2 + 2^2、
13 = 2^2 + 3^2、
17 = 1^2 + 4^2、
29 = 2^2 + 5^2
という風に、
2 つの平方数(二乗した数のこと)に分解できることです。
ここで、4^2 とは、4 の二乗を表したつもりです。
「二乗」とは自分自身を 2 回掛けるという操作のことで、たとえば 5^2 は 25 (= 5×5) になります。
もちろん、これら 5、13、17、29は適当に選んだのではなく、ある共通の特徴があります。
それは、4 で割ると 1 余ること。
用するに、
「4 で割ると 1 余る素数は 2 つの平方数の和に分解できる」
のです。
もちろん、29 以降の素数にもこの性質は成り立っており、たとえば
157 = 6^2 + 11^2、
569 = 13^2 + 20^2、
3137 = 1^2 + 56^2、
6065 = 17^2 + 76^2、
45572521 = 2464^2 + 6285^2
10000000000037 = 1791119^2 + 2606126^2
となります。
さて、ではなぜこのようなことが成り立つかということですが、
私の知っている証明法ではどうしても Gauss 素数(素数の複素数版)とやらの知識を用意しなければならないため、ここでは割愛させていただきます。
こんな話が面白いと感じたあなたは、すでに素数(または数学)の虜です。
のめり込むのもいいですが、いつでも戻ってこれるようにほどほどにして下さいね!
今日はこんなとことです。Posted by hnfs.
整数 p が素数であるとは、
p が 1または p 自身以外に約数を持たないことを言います。
たとえば、2 の約数は 1 と 2 のみなので、2 は素数です。
そして、13 や 71 なども素数になります。
逆に、4 は 2 を約数に持つ(すなわち、1 と自分自身の 4 以外の約数を持つ)ので、素数ではありません。ちなみに、1 も素数ではないと約束します。
この素数とやらは数々の魅力的な性質を持っており、これまで多くの数学者を虜にしてきたようです。
そこで、今回はその不思議な性質の 1 つを紹介したいと思います。
素数をいくつか列挙してみます。
2、3、5、7、11、13、17、19、23、29、31…
これくらいにしておきましょう。
これらの素数のうち、
5、13、17、29
には、ある性質があります。
それは、
5 = 1^2 + 2^2、
13 = 2^2 + 3^2、
17 = 1^2 + 4^2、
29 = 2^2 + 5^2
という風に、
2 つの平方数(二乗した数のこと)に分解できることです。
ここで、4^2 とは、4 の二乗を表したつもりです。
「二乗」とは自分自身を 2 回掛けるという操作のことで、たとえば 5^2 は 25 (= 5×5) になります。
もちろん、これら 5、13、17、29は適当に選んだのではなく、ある共通の特徴があります。
それは、4 で割ると 1 余ること。
用するに、
「4 で割ると 1 余る素数は 2 つの平方数の和に分解できる」
のです。
もちろん、29 以降の素数にもこの性質は成り立っており、たとえば
157 = 6^2 + 11^2、
569 = 13^2 + 20^2、
3137 = 1^2 + 56^2、
6065 = 17^2 + 76^2、
45572521 = 2464^2 + 6285^2
10000000000037 = 1791119^2 + 2606126^2
となります。
さて、ではなぜこのようなことが成り立つかということですが、
私の知っている証明法ではどうしても Gauss 素数(素数の複素数版)とやらの知識を用意しなければならないため、ここでは割愛させていただきます。
こんな話が面白いと感じたあなたは、すでに素数(または数学)の虜です。
のめり込むのもいいですが、いつでも戻ってこれるようにほどほどにして下さいね!
今日はこんなとことです。Posted by hnfs.
そんなに大きくなりませんよ
2010年4月18日 数学
おかしな問題を見つけたので、紹介したいと思います。
どこかおかしいのかというと…
「ΔABCの面積は決して84にはなりえない」
ということなんです。気づきましたか?
一応理由を説明しておくと、
ΔABCの面積は縦 8、横9の長方形の面積より小さくなることが、右下図より直感的にわかると思います。
そのため、
ΔABCの面積 < (長方形の面積) = 8×9 = 72 < 84
となるのです。
これはかなり大雑把な評価なんですけどね。
一応、この問題が求める答えを求めてはみましたが…
最初は混乱しましたよ。「こんなのありえねぇよ…」ってね。
「数式なんて見るのもいやだ」または「こんな問題簡単だ」という方は次の引用部を飛ばしていただいても結構です。
まぁ、そんなこんなで(出題者側が意図していたであろう)答えは7なんですけど、なぜΔABCの面積を84にしてしまったのでしょうかね?
出題者は問題の解き方だけを知っていて、数字は適当に設定したのではないかと疑いたくなってしまいますね。
ちなみにこの問題が出題された試験は受験者もまぁまぁ多く、公共性も一応高いと思われる試験なんですけどね…。
さて、揚げ足取りはこのへんにしておきましょうか。
今日はこんなとろです。Posted by hnfs.
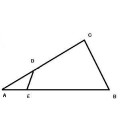
右上図のΔABCで、
AB = 9、AC = 8、AD = 3、AE = 2
とします。
また、ΔABCの面積を84とします。
このとき、ΔADEの面積を求めなさい。
どこかおかしいのかというと…
「ΔABCの面積は決して84にはなりえない」
ということなんです。気づきましたか?
一応理由を説明しておくと、
ΔABCの面積は縦 8、横9の長方形の面積より小さくなることが、右下図より直感的にわかると思います。
そのため、
ΔABCの面積 < (長方形の面積) = 8×9 = 72 < 84
となるのです。
これはかなり大雑把な評価なんですけどね。
一応、この問題が求める答えを求めてはみましたが…
最初は混乱しましたよ。「こんなのありえねぇよ…」ってね。
「数式なんて見るのもいやだ」または「こんな問題簡単だ」という方は次の引用部を飛ばしていただいても結構です。
一般に、ΔABCの面積Sは
S = (1/2) * AB * AC * sinA
で求めることができることを確か高校生で習ったかと思います。
なぜこの式で求められるのか気になる方がいれば、コメントに「ラクト珈琲」の文字を混入させてください。
これを用いると…
ΔABC = (1/2) * AB * AC * sinA = (1/2) * 9 * 8 * sinA = 36sinA
ΔADE = (1/2) * AD * AE * sinA = (1/2) * 3 * 2 * sinA = 3sinA
となります。
これを比で考えると、
ΔABC : ΔADE = 36sinA : 3sinA = 12 : 1
となります。ΔABCの面積は84であることから、
84 : ΔADE = 12 : 1 ⇔ ΔADE = 7
となり、ΔADEの面積は7であることがわかります。
まぁ、そんなこんなで(出題者側が意図していたであろう)答えは7なんですけど、なぜΔABCの面積を84にしてしまったのでしょうかね?
出題者は問題の解き方だけを知っていて、数字は適当に設定したのではないかと疑いたくなってしまいますね。
ちなみにこの問題が出題された試験は受験者もまぁまぁ多く、公共性も一応高いと思われる試験なんですけどね…。
さて、揚げ足取りはこのへんにしておきましょうか。
今日はこんなとろです。Posted by hnfs.
こんなタイトルにしてしまいました…。ゴメンなさい!
ちなみに、「とあるすうがくのコントラディクション」と読ませます。
今回は、数学のトピックを取り上げたいと思います。
上図の正方形をご覧ください。この正方形の一辺の長さを1とします。
このとき、黒太線の長さは何でしょうか?
そうです。
√2 (ルート2)ですね。覚えておいてくださいね。
黒太線と赤太線で囲まれる直角(二等辺)三角形に三平方の定理を用いて導けます。念のため。
(直角二等辺三角形の辺の比は 1:1:√2 であることを中学校でやったことを思い出せれば、それで結構です。)
さて、問題はここから。
上図の正方形の赤太線の長さはいくらになるでしょうか?
そうです。2 ですね。
では、中図の正方形(もちろんこれも一辺の長さは1)の赤太線の長さはいくらでしょうか?
そうです。これまた 2 なのです。
ではでは、下図の正方形(もちろん一辺長1)の赤太線の長さはいくらでしょうか?
そうです。またしても 2 なのです。
上図→中図→下図の流れの法則性はお気づきですか?
下図の黄色→黄土色→オレンジ→赤の流れのように、黒太線に沿って階段の段数を倍々にしているのです。
そして、いずれの色の太線も、トータルの長さは 2 なのです。
では、核心部分へ。
このような階段作りの操作を無限に繰り返しても、細かい階段を構成する太線の長さは 2 になるでしょう。
そして、この操作を無限に繰り返すことは、階段を限りなく黒太線に近づけることを意味します。
ということは、きっと黒太線の長さは 2 になるでしょう・・・
いやいや!思い出してください。
黒太線の長さは、√2 でした。
ということは、まさか √2 = 2 ということに・・・?
いやいや、もちろんそんなことはないですよ。調べたら分かりますが、
√2 ≒ 1.41421356…
です。
どこかがおかしいのです。
答えは用意していませんよ~
今日はこんなところです。Posted by hnfs.
ちなみに、「とあるすうがくのコントラディクション」と読ませます。
今回は、数学のトピックを取り上げたいと思います。
上図の正方形をご覧ください。この正方形の一辺の長さを1とします。
このとき、黒太線の長さは何でしょうか?
そうです。
√2 (ルート2)ですね。覚えておいてくださいね。
黒太線と赤太線で囲まれる直角(二等辺)三角形に三平方の定理を用いて導けます。念のため。
(直角二等辺三角形の辺の比は 1:1:√2 であることを中学校でやったことを思い出せれば、それで結構です。)
さて、問題はここから。
上図の正方形の赤太線の長さはいくらになるでしょうか?
そうです。2 ですね。
では、中図の正方形(もちろんこれも一辺の長さは1)の赤太線の長さはいくらでしょうか?
そうです。これまた 2 なのです。
ではでは、下図の正方形(もちろん一辺長1)の赤太線の長さはいくらでしょうか?
そうです。またしても 2 なのです。
上図→中図→下図の流れの法則性はお気づきですか?
下図の黄色→黄土色→オレンジ→赤の流れのように、黒太線に沿って階段の段数を倍々にしているのです。
そして、いずれの色の太線も、トータルの長さは 2 なのです。
では、核心部分へ。
このような階段作りの操作を無限に繰り返しても、細かい階段を構成する太線の長さは 2 になるでしょう。
そして、この操作を無限に繰り返すことは、階段を限りなく黒太線に近づけることを意味します。
ということは、きっと黒太線の長さは 2 になるでしょう・・・
いやいや!思い出してください。
黒太線の長さは、√2 でした。
ということは、まさか √2 = 2 ということに・・・?
いやいや、もちろんそんなことはないですよ。調べたら分かりますが、
√2 ≒ 1.41421356…
です。
どこかがおかしいのです。
答えは用意していませんよ~
今日はこんなところです。Posted by hnfs.